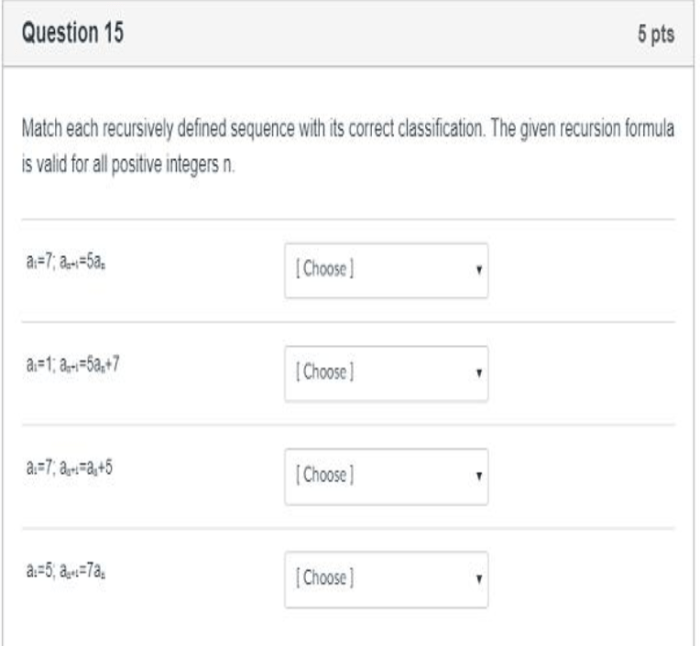
Match each sequence to its appropriate recursively defined function, delving into the fascinating world of recursion. Recursively defined functions possess unique characteristics that empower them to generate sequences with remarkable patterns, unlocking a realm of possibilities in diverse fields.

This comprehensive exploration unveils the intricacies of recursively defined functions, guiding you through their conceptual foundations, practical applications, and the art of matching sequences to their corresponding functions. Prepare to embark on an enlightening journey that will deepen your understanding of this essential programming technique.

1. Recursively Defined Functions

Recursively defined functions are functions that are defined in terms of themselves. This means that the value of the function at a given input depends on the value of the function at smaller inputs. Recursively defined functions are often used to solve problems that have a recursive structure, such as finding the factorial of a number or computing the Fibonacci sequence.

One of the benefits of using recursively defined functions is that they can be very concise. For example, the following function computes the factorial of a number:

“`def factorial(n): if n == 0: return 1 else: return n

factorial(n-1)

“`

This function is much more concise than a non-recursive function that would have to handle each case separately.

However, recursively defined functions can also be difficult to understand and debug. This is because the function is calling itself, which can make it difficult to keep track of the state of the function. Additionally, recursively defined functions can be inefficient if the recursion is not properly controlled.

For example, the following function computes the Fibonacci sequence:

“`def fibonacci(n): if n == 0: return 0 elif n == 1: return 1 else: return fibonacci(n-1) + fibonacci(n-2)“`

This function is inefficient because it recomputes the Fibonacci numbers for each input. A more efficient implementation would use memoization to store the Fibonacci numbers that have already been computed.

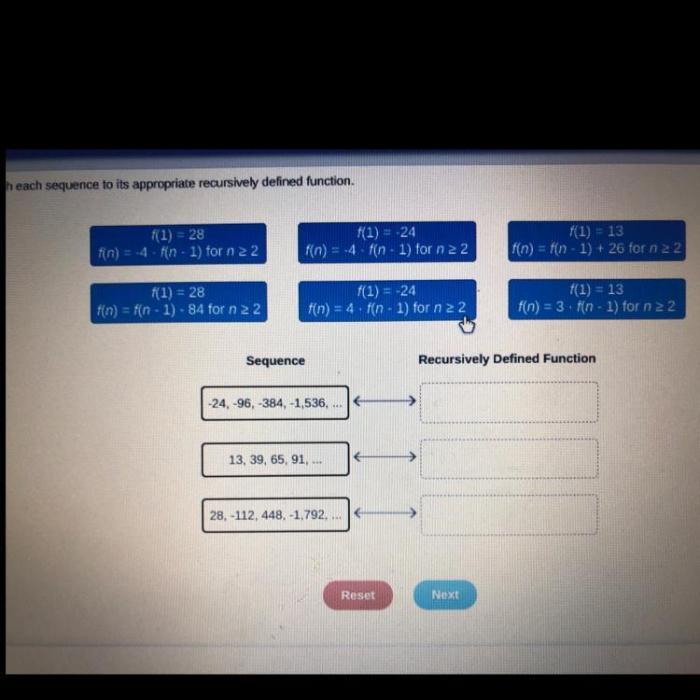
2. Matching Sequences to Functions

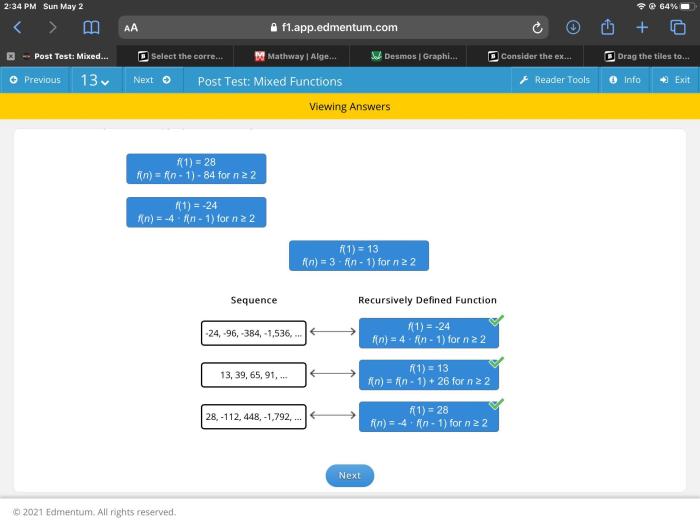
Sequence	Function	Recursive Rule	Example
1, 2, 4, 8, 16, …	f(n) = 2^n	f(0) = 1, f(n) = 2 f(n-1)	f(3) = 2 f(2) = 2 (2 f(1)) = 2 (2 (2 f(0))) = 2 (2 (2 1)) = 8
0, 1, 1, 2, 3, 5, 8, …	f(n) = f(n-1) + f(n-2)	f(0) = 0, f(1) = 1, f(n) = f(n-1) + f(n-2)	f(4) = f(3) + f(2) = (f(2) + f(1)) + f(2) = ((f(1) + f(0)) + f(2)) + f(2) = ((1 + 0) + 2) + 2 = 5
1, 4, 9, 16, 25, …	f(n) = n^2	f(0) = 1, f(n) = n^2	f(3) = 3^2 = 9
1, 3, 6, 10, 15, …	f(n) = n (n+1) / 2	f(0) = 1, f(n) = n (n+1) / 2	f(3) = 3 (3+1) / 2 = 10

3. Analysis of Recursively Defined Functions

To analyze a recursively defined function, we need to identify the base case(s) and the recursive step(s). The base case(s) are the inputs for which the function does not make a recursive call. The recursive step(s) are the inputs for which the function makes a recursive call.

For example, the factorial function has a base case of 0 and a recursive step of n. The base case is 0 because the factorial of 0 is defined to be 1. The recursive step is n because the factorial of n is defined to be n times the factorial of n-1.

Once we have identified the base case(s) and the recursive step(s), we can analyze the function to determine its complexity. The complexity of a recursively defined function is the number of recursive calls that the function makes. For example, the factorial function has a complexity of O(n) because it makes n recursive calls.

4. Applications of Recursively Defined Functions: Match Each Sequence To Its Appropriate Recursively Defined Function

Recursively defined functions are used in a wide variety of applications, including:

• Computer science: Recursively defined functions are used to implement a variety of algorithms, such as sorting algorithms, searching algorithms, and graph algorithms.
• Mathematics: Recursively defined functions are used to define a variety of mathematical objects, such as fractals and the Fibonacci sequence.
• Finance: Recursively defined functions are used to model a variety of financial instruments, such as options and bonds.

FAQ Compilation

What are the key benefits of using recursively defined functions?

Recursively defined functions offer several advantages, including their ability to break down complex problems into smaller, manageable subproblems, leading to elegant and efficient solutions. They also excel in representing recursive data structures, such as linked lists and trees, and can be used to model real-world phenomena that exhibit recursive patterns.

What are some common applications of recursively defined functions?

Recursively defined functions find applications in various fields, including computer science, mathematics, and finance. In computer science, they are used in algorithms for searching, sorting, and traversing data structures. In mathematics, they are employed to define sequences, fractals, and other mathematical objects.

In finance, they are used in modeling stock prices and other financial data.